前言

实验室一直在用到推荐系统，其中最重要的一部分就是利用近似最近邻算法（ANN）在大量论文/专利/项目中找到最相似的的论文/专利/项目进行推荐。

之前的 ANN 算法一直是 gensim 中使用的 Annoy。但是鉴于基于图的 HNSW 在 ANN Benchmarks 中的优异表现，需要对其进行学习并且进行一定修改，最后应用到推荐系统中。

KNN 和 ANN

k-Nearest Neighbor, KNN
- K最近邻算法，可用作聚类、回归等。
Approximate nearest neighbor, ANN
- 目前在高维度度量空间中没有有效精确 NNS 的方法。这背后的原因在于维度的“诅咒” 。为了避免维数的诅咒，减少对 kNN 问题解决方案的要求，使其近似（ANN），精度允许的条件下通过牺牲准确率来换取比暴力搜索要快的多的搜索速度。
- ANN 应用：推荐系统。

HNSW 文章：

ANN 方法分类

树方法，如 KD-tree
哈希方法，如 Local Sensitive Hashing (LSH)
矢量量化方法，如 Product Quantization (PQ)
近邻图方法，如 Hierarchical Navigable Small World (HNSW)

HNSW

分层的可导航小世界（Hierarchical Navigable Small World, HNSW）。

特点

一种基于图的数据结构。
使用贪婪搜索算法的变体进行ANN搜索，每次选择最接近查询的未访问的相邻元素时，它都会从元素到另一个元素地遍历整个图，直到达到停止条件。

Delaunay 三角剖分

Delaunay 三角剖分（Delaunay triangulation）是学习 HNSW 的预备知识，具体见我之前有学习过的：Voronoi 图和 Delaunay 三角剖分。HNSW 的生成的索引在最后的形式将会是近似的 Delaunay 图，只是由于 HNSW 具有 可导航（Navigable）的属性，最后生成的图在搜索时会具有一些长边（Long-range edges）来进行快速逼近目标点。

Delaunay 边
- 存在一个圆经过 $a, b$ 两点，圆内（注意是圆内，圆上最多三点共圆）不含点集 $V$ 中任何其他的点，这一特性又称空圆特性。
Delaunay 三角剖分
- 如果点集 $V$ 的一个三角剖分 $T$ 只包含 Delaunay 边，那么该三角剖分称为 Delaunay 三角剖分。

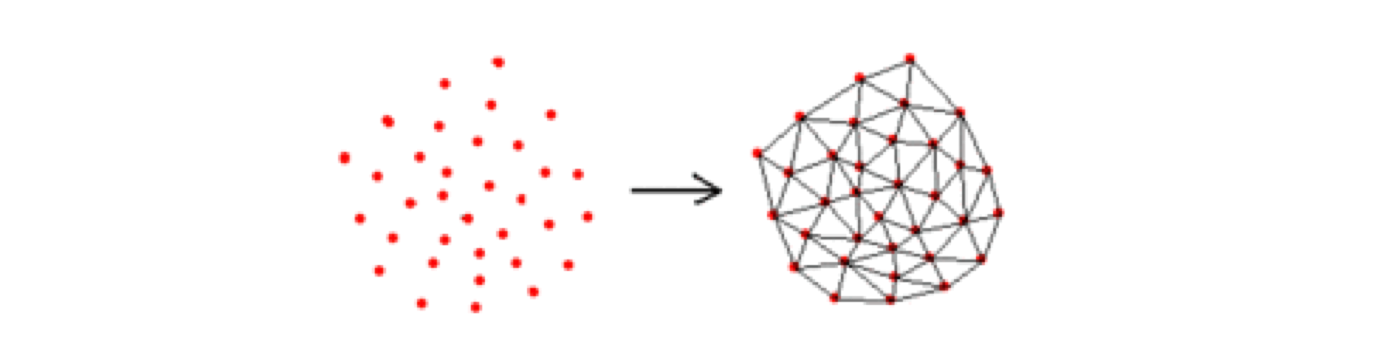
NSW 主要思想

要理解 Hierarchical NSW，要先理解 NSW，即没有分层的可导航小世界的结构。

对于每个新的传入元素，我们从结构中找到其最近邻居的集合（近似的 Delaunay 图）。该集合连接到元素。随着越来越多的元素被插入到结构中，以前用作短距离边现在变成长距离边，形成可导航的小世界。

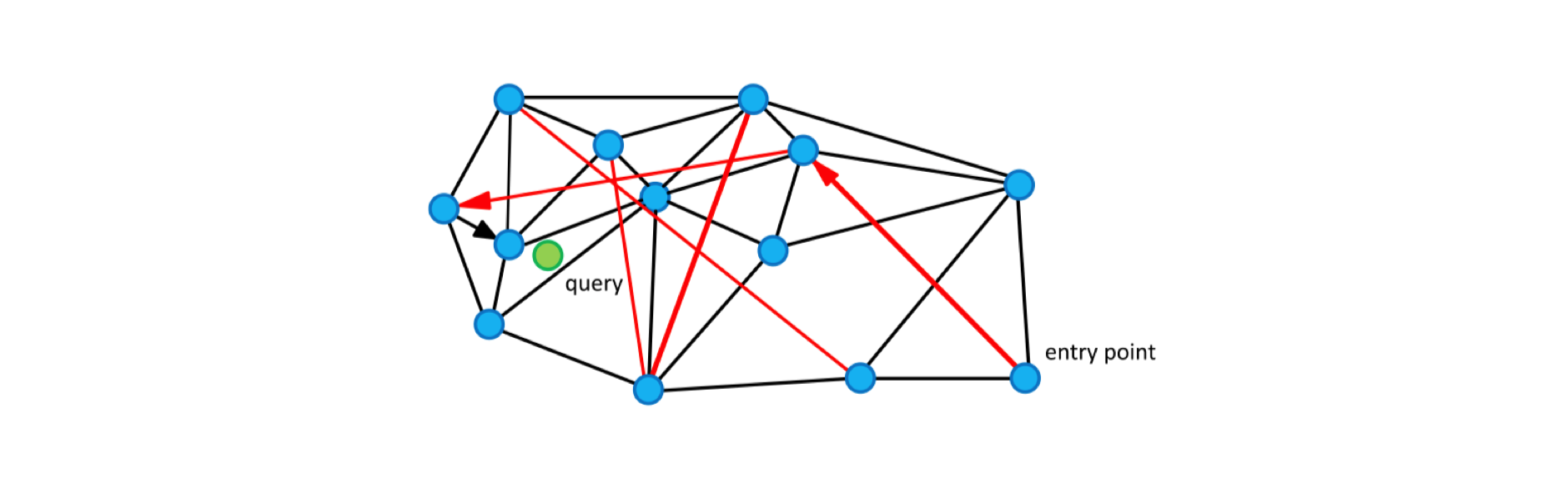
圆（顶点）是度量空间中的数据，黑边是近似的 Delaunay 图，红边是用于对数缩放的长距离边。箭头显示从入口点到查询的贪心算法的示例路径（显示为绿色）。

图中的边有两个不同的目的：

Short-range edges，用作贪婪搜索算法所需的近似 Delaunay 图。
Long-range edges，用于贪婪搜索的对数缩放。负责构造图形的可导航小世界（NSW）属性。

NSW 中的贪婪搜索

算法计算从查询 $q$ 到当前顶点的朋友列表的每个顶点的距离，然后选择具有最小距离的顶点。
如果查询与所选顶点之间的距离小于查询与当前元素之间的距离，则算法移动到所选顶点，并且它变为新的当前顶点。
算法在达到局部最小值时停止：一个顶点，其朋友列表不包含比顶点本身更接近查询的顶点

NSW K-NNSearch 算法伪代码

K-NNSearch(object q, integer: m, k)
TreeSet [object] tempRes, candidates, visitedSet, result 
// 进行m次循环，避免随机性
for (i←0; i < m; i++) do:
    put random entry point in candidates
    tempRes←null
    repeat:
        // 利用上述提到的贪婪搜索算法找到距离q最近的点c
        get element c closest from candidates to q
        remove c from candidates
        // 判断结束条件
        if c is further than k-th element from result then
            break repeat
        // 更新后选择列表
        for every element e from friends of c do:
            if e is not in visitedSet then
                add e to visitedSet, candidates, tempRes
    end repeat
    // 汇总结果
    add objects from tempRes to result 
end for 
return best k elements from result

Hierarchical Navigable Small World (HNSW)

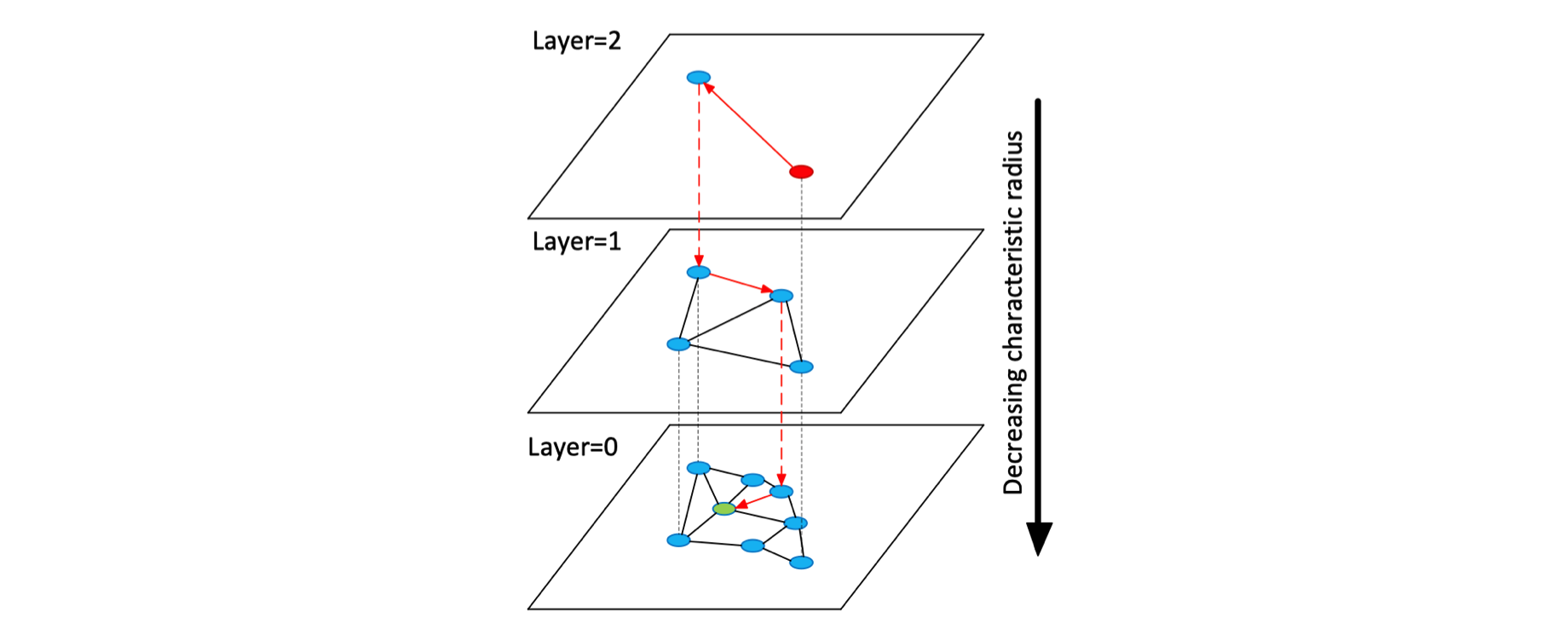
该算法贪婪地遍历来自上层的元素，直到达到局部最小值。
之后，搜索切换到较低层（具有较短 link），从元素重新开始，该元素是前一层中的局部最小值，并且该过程重复。
通过采用层状结构，将边按特征半径进行分层，从而将 NSW 的计算复杂度由多重对数（Polylogarithmic）复杂度降到了对数（logarithmic）复杂度。

HNSW 的具体源码实现现在还在学习中。

Hello World!

近似最近邻算法 HNSW 学习笔记（一）介绍

前言